Оригами-тетраэдр из бумаги – эффектный и многофункциональный декоративный элемент. В зависимости от модели, он может служить интерьерной подвеской, ёлочным украшением и частью модного настенного панно в скандинавском стиле. Тетраэдр – четырёхгранная пирамида, в основании которой лежит треугольник. Чаще всего для декора используют несколько таких фигур, объединённых в композицию.
Как сделать объемные геометрические фигуры из бумаги (схемы, шаблоны)?
Вот несколько схем, по которым можно изготовить объёмные геометрические фигуры.
Самая простая — тетраэдр.
Чуть сложнее будет изготовить октаэдр.
А вот эта объёмная фигура — додекаэдр.
Ещё одна — икосаэдр.
Более подробно об изготовлении объёмных фигур можно посмотреть здесь.
Вот так выглядят объёмные фигуры не в собранном виде:
А вот так выглядят уже готовые:
Из объёмных геометрических фигур можно сделать много оригинальных поделок, в том числе и упаковки для подарка.
Чтобы дети лучше запомнили, какие бывают геометрические фигуры, и знали, как они называются, можно из плотной бумаги или картона сделать объемные геометрические фигуры. Кстати, на основе их можно изготовить красивую подарочную упаковку.
- плотная бумага, либо картон (лучше цветные);
- линейка;
- карандаш;
- ножницы;
- клей (лучше ПВА).
Самое сложное — это разработать и начертить развёртки, нужны хотя бы базовые знания черчения. Можно взять и готовые развёртки и распечатать на принтере.
Чтобы линия сгиба была ровной и острой, можно воспользоваться тупой иглой и металлической линейкой. При проведении линии иголку нужно сильно нагнуть в направлении движения, практически положив её набок.
Это развертка трехгранной пирамиды
Это развертка куба
Это развертка октаэдра (четырехгранной пирамиды)
Это развертка додекаэдра
Это развертка икосаэдра
Вот здесь можно найти шаблоны более сложных фигур (Платоновы Тела, Архимедовы тела, многогранники, полиэдры, разные виды пирамид и призм, простые и косые бумажные модели).
Кстати, чтобы рассчитать параметры пирамиды, можно воспользоваться вот этой программой.
Самостоятельно смастерив из бумаги объёмные фигуры можно не только использовать их для развлечения, но и для обучения.
К примеру, можно наглядно показать ребёнку как выглядит та или иная фигура, дать её подержать в руках.
Либо можно с целью обучения распечатать схемы со специальными обозначениями.
Так предлагаю ниже ознакомиться со семой додекаэдра, как простой, так и с небольшими рисунками, которые только привлекут внимание малыша и обучение сделают более весёлым и занимательным.
Также схему куба можно использовать для обучения цифрам.
Схема пирамиды может помочь усвоить формулы, которые относятся к данной фигуре.
Кроме того, предлагаю ознакомиться со схемой октаэдра.
Схема тетраэдра помимо прочего поможет изучить цвета.
Как вы поняли, вышеприведённые шаблоны необходимо распечатать, вырезать, согнуть по линиям, склеить по специальным узким полосочкам, прилегающим к избранным сторонам.
Прежде чем начать делать объемные геометрические фигуры, нужно представить (или знать как выглядит) фигуру в 3D измерении: сколько граней имеет та или иная фигура.
Сначала необходимо правильно начертить на бумаге фигуру по граням, которые должны быть соединены между собой. У каждой фигуры грани имеют определенную форму: квадрат, треугольник, прямоугольник, ромб, шестиугольник, круг и т.д.
Очень важно, чтобы длина ребер фигуры, которые будут соединены друг с другом имели одинаковую длину, чтобы во время соединения не возникло проблем. Если фигура состоит из одинаковых граней, я бы предложила сделать шаблон во время черчения использовать этот шаблон. Так же можно скачать из интернета готовые шаблоны, распечатать их, согнуть по линиям и соединить (склеить).
Японское изобретение
Настоящей головоломкой может стать не только сам куб, изобретенный японским ученым Наоки Йошимото в 1971 году, но и сборка этого необычного изделия. По данной схеме нужно собрать 48 пирамидок.
Как правильно собрать эту чудесную поделку и о ее трансформациях, вы можете наглядно посмотреть в данном видеоуроке:
Пирамида — развертка. Развертка пирамиды для склеивания. Развертки из бумаги
Прямоугольник, квадрат, треугольник, трапеция и другие – геометрические фигуры из раздела точной науки. Пирамида — это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции. Для полного представления и изучения любого геометрического объекта изготавливают макеты. Используют самый разнообразный материал, из которого выполняется пирамида. Поверхность многогранной фигуры, развернутая на плоскости, называется ее разверткой. Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии. Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.
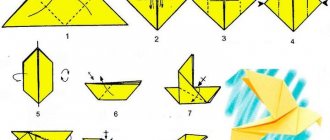
Модульный треугольник
Для сборки лучше воспользоваться большим листом формата А4, а затем конструировать из мелких заготовок. Соотношение сторон для модуля – 1:1,5.
- Лист складывается пополам по горизонтали, пальцами по вертикали проглаживается серединная линия, концы сгибаются к центральной наметке.
- Модуль переворачивается, края-ушки поднимаются кверху.
- Через основную часть фигуры нужно загнуть боковые уголки.
- Основа распрямляется, по линиям формируются маленькие треугольники с поднятыми вверх краешками. Основание сгибается пополам.
Полученные модули снабжены парой уголков и кармашками, комбинируя которые, по-разному вставляя друг в друга, можно собирать разнообразные объемные изделия.
Определение параметров
Прежде всего определим, какой будет пирамида. Развертка данной фигуры является основой для изготовления объемной фигуры. Выполнение работы потребует предельной точности. При неправильном чертеже геометрическую фигуру собрать будет невозможно. Допустим, необходимо изготовить макет правильной треугольной пирамиды.
Любое геометрическое тело обладает определенными свойствами. Данная фигура имеет основанием правильный многоугольник, а ее вершина спроецирована в его центр. В качестве основания выбран равносторонний треугольник. Данное условие определяет название. Боковые ребра у пирамиды – это треугольники, количество которых зависит от выбранного для основания многогранника. В данном случае их будет три. Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Развертки из бумаги выполняются в соответствии с учетом всех данных геометрической фигуры. Параметры будущей модели оговариваются заранее. От этих данных зависит выбор используемого материала.
Сложный параллелепипед
Параллелепипед — сложная фигура многогранник, у которого 6 граней и каждая из них параллелограмм.
Чтобы сделать параллелепипед техникой оригами, нужно начертить основание — параллелограмм любого размера. С каждой его стороны нарисовать боковые стороны — тоже параллелограммы. Далее от любой из боковых сторон дорисовать второе основание. Добавить места для склеивания. Параллелепипед может быть прямоугольным, если все стороны имеют прямые углы. Затем вырезать развертку и склеить. Готово!
Как выполняется развертка правильной пирамиды?
Основой модели является лист бумаги или картона. Работу начинают с чертежа пирамиды. Фигура представляется в развернутом виде. Плоское изображение на бумаге соответствует заранее выбранным размерам и параметрам. Правильная пирамида имеет основанием правильный многоугольник, а высота проходит через его центр. Изготавливаем для начала простую модель. В данном случае – это треугольная пирамида. Определяем размеры выбранной фигуры.
Интересные факты
Тетраэдр – одно из самых интересных, с точки зрения коммерции, платоновых тел. Достаточно простая пирамидка известна каждому с детства. В таких треугольных пакетах – тетропаках во времена СССР продавали молоко, кефир и сливки. Считалось, что благодаря пирамидальной форме деликатная продукция дольше сохраняется свежей.
Треугольная упаковка – совсем не советское изобретение. В 1930-х годах французский научно-популярный журнал «Science & Vie» опубликовал статью о загадочных свойствах египетских пирамид, где тела фараонов не портились, а мумифицировались естественным путём. Теория не подкреплялась серьёзными доказательствами, однако шведский изобретатель Эрик Валленберг настолько увлёкся ею, что создал мини-аналог древнеегипетских усыпальниц – ту самую картонную упаковку Tetra Classic. Он хотел снизить потери молокоторговцев, но на деле оказал помощь производителям одноразовой тары. Его пирамидки выпускались быстро, в больших объёмах и практически без отходов.
В 1950 году на базе инновационной технологии была создана компания AB Tetra Pak. Однако, когда выяснилось, что продукция в картонных пирамидках скисает почти так же быстро, как в стеклянных бутылках, шведы утратили интерес к идее Валленберга. Тем не менее, технологию производства удалось продать советскому руководству, делая упор на её бюджетность и эффективность. Так на наших прилавках появились легендарные «треугольнички» с надписью «Молоко». Чтобы транспортировка пакетов-тетраэдров была не менее выгодной, чем производство, под них изготовили специальные шестиугольные контейнеры.
Сегодня трёхмерные треугольные пакеты (точнее, пакетики) взяла на вооружение компания Lipton. Производитель утверждает, что заменяет плоскую порционную упаковку объёмной, чтобы продемонстрировать красоту раскрывшегося в чашке чайного листа. И показать, что в пакетиках не обрезки и крошка, как подозревают потребители, а полноценный качественный купаж.
Развертка четырехугольной пирамиды
Сначала представим, как выглядит геометрическая фигура, макет которой будем изготавливать. Основанием выбранной пирамиды является четырехугольник. Боковые ребра — треугольники. Для работы используем те же материалы и приспособления, что и в предыдущем варианте. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами.
Каждую сторону основания делим пополам. Проводим перпендикуляр, который будет являться высотой треугольной грани. Раствором циркуля, равным длине боковой грани пирамиды, делаем на перпендикулярах засечки, установив его ножку в вершину основания. Оба угла одной стороны основания соединяем с полученной точкой на перпендикуляре. В результате получаем в центре чертежа квадрат, на гранях которого нарисованы треугольники. Чтобы зафиксировать модель на боковых гранях, дорисовывают вспомогательные клапаны. Для надежного крепления достаточно полоски сантиметровой ширины. Пирамида готова к сборке.
Пошаговая инструкция письма «Треугольничек заветный»
Таким приемом могут воспользоваться: воспитатели детских садов, педагоги и родители. Треугольники можно подарить ветерану. Он послужит экспонатом на выставке поделок или будет частью стенгазеты военной тематики.
Создавая открытку с поздравлением, подрастающее поколение получает навыки обращения с бумагой, ножницами и клеем. У детей развиваются творческие способности и воображение. Помимо этого, приобретается усидчивость, и воспитывается чувство патриотизма.
Материалы
Необходимо заблаговременно заготовить:
- Разноцветные листы бумаги.
- Ножницы.
- Клей.
- Георгиевскую ленточку.
- Пластилин.
- Пакетик чая или растворимый кофе.
Соблюдение безопасности с ножницами
- Никогда не оставлять их раскрытыми.
- Передача только кольцами вперед.
- Ни в коем случае не играть.
- Использовать исключительно по мере надобности.
Правила работы с клеем ПВА
- Пользоваться кисточкой.
- Избегать набора излишков, ненужное удаляется салфеткой из бумаги.
- Осторожное нанесение тонким слоем.
- Не допускать попаданий на предметы одежды, лицо и в глаза.
- По завершении действий тюбик плотно закрывается и хранится в укромном месте.
- Руки и место, за которым работали, моют с мылом.
При оформлении для большей правдоподобности прибегают к разным оттенкам и «рельефности», чтобы «состарить» бумагу. Слова, которые автор выбрал в качестве поздравления, распечатываются и промокаются при помощи губки с 2-х сторон. Далее по всей поверхности листа посыпается кофе, крупинки которого растворяются смоченным кусочком поролона. Лист остается сохнуть.
Для придания торжественного момента послания дорогим участникам военных событий в виде треугольника не возбраняется украсить, составив композицию из соответствующих атрибутов. У георгиевской ленточки измеряется определенная длина, затем она прикладывается к уголку бумаги в форме треугольника, отрезается и приклеивается. Из белой бумаги вырезаются ромашки, края которых загибаются карандашом.
Ножницами из зеленой бумаги формируются листья. Стебельки располагаются на георгиевской ленте, приклеиваются цветы и листья. Средние части декорируются желтым пластилином, который необходимо скатать шариками. Чтобы они эффектно смотрелись, их нужно немного придавить.
В качестве дополнения прилагается надпись, аналогичным образом обработанная заваренным пакетиком чая. Подобные «треугольнички» солдаты всегда с нетерпением ожидали, как заветную весточку из дома, а затем по много раз перечитывали.
Построение чертежа
Развертка пирамиды усеченной выполняется в несколько этапов. Боковой гранью усеченной пирамиды является трапеция, а основаниями — подобные многогранники. Допустим, что это квадраты. На листе бумаги выполняем чертеж трапеции с заданными размерами. Боковые стороны полученной фигуры продлеваем до пересечения. В результате получаем равнобедренный треугольник. Его сторону измеряем циркулем. На отдельном листе бумаги строим окружность, радиусом которой будет измеренное расстояние.
Следующий этап – это построение боковых ребер, которые имеет усеченная пирамида. Развертка выполняется внутри нарисованной окружности. Циркулем измеряют нижнее основание трапеции. На окружности отмечаем пять точек, которые соединяют линии с ее центром. Получаем четыре равнобедренных треугольника. Циркулем измеряем сторону трапеции, нарисованной на отдельном листе. Данное расстояние откладываем на каждой стороне нарисованных треугольников. Полученные точки соединяем. Боковые грани трапеции готовы. Остается только нарисовать верхнее и нижнее основания пирамиды. В данном случае это подобные многогранники – квадраты. К верхнему и нижнему основаниям первой трапеции дорисовываем квадраты. На чертеже изображены все части, которые имеет пирамида. Развертка практически готова. Остается только дорисовать соединительные клапаны на сторонах меньшего квадрата и одной из граней трапеций.
Бумажная модель
Используя 30 квадратных листов бумаги (размер каждой стороны 7,5 см), можно сделать довольно крепкую версию одной из разновидности этого геометрического чуда совсем без склеивания. Если в запасе есть материал разного цвета, то получится яркий и красивый макет с разноцветными блоками. Инструкция по изготовлению звездчатого икосаэдра поэтапно:
- Сложить листок пополам и сделать складку вдоль сгиба. Если используется бумага для оригами, то стоит убедиться, что её лицевая сторона находится снаружи, поскольку она будет видна позже.
- Развернуть квадрат.
- Сложить правую и левую стороны листа так, чтобы они встретились в месте сгиба. Должен получиться прямоугольник, больше похожий на шкаф с распашными дверцами.
- Перевернуть фигуру подогнутыми краями вниз.
- Сделать диагональную складку: верхний правый угол должен встретиться с левой стороной прямоугольника. Нужно свернуть обе «двери шкафа».
- Перевернуть бумагу прямым концом вверх.
- Сделать ещё одну диагональную складку, где верхний правый угол будет встречаться со стороной макета. Должен получиться параллелограмм.
- Согнуть лист по диагонали там, где верхний угол соответствует правому углу фигуры.
- Повторить действие с другой стороны. Должны встретиться нижний и левый углы. Получится маленький квадрат.
- Затем повернуть заготовку так, чтобы фигура напоминала ромб.
- Сложить квадрат пополам, сделав сгиб, который идёт перпендикулярно «дверцам шкафа», видимым на модели. Итак, первая единица готова.
Всего таких блоков нужно сделать 30. Например, по 10 разного цвета.
Развёртки геометрических фигур
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров